激光扩束器

激光扩束器设计用于扩大平行输入光束的直径较大的平行输出光束。激光扩束器常用于如激光扫描、干涉测量或遥测应用中。现在的激光扩束器都是采用从完善的光学望远镜基础中发展而来的无焦系统设计。在此类系统中，位于无穷远的物体光线，以平行的方式进入内部光学件的光轴中，同时也以平行的方式离开。这意味着整个系统不具备焦距。

理论：望远镜

传统上，光学望远镜主要用于观察远处的目标，例如宇宙中的天体。光学望远镜主要可分为两大类：折射望远镜和反射望远镜。折射望远镜充分利用透镜来折射或弯曲光线，而反射望远镜则是利用反射镜来反射光线。

折射望远镜可分为以下两类：开普勒式望远镜和伽利略式望远镜。开普勒式望远镜由焦距为正的透镜组合而成，而透镜是通过焦距总和分割（图1）。离来源图像或被观察物体近的透镜被称为物镜，而靠近人眼或成像的透镜则成为成像透镜。

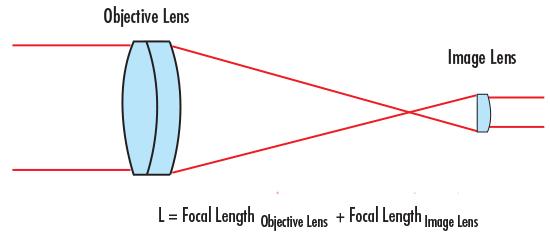
图1: 开普勒式望远镜

伽利略式望远镜由正透镜和负透镜组合而成，透镜也是通过焦距总和分割（图2）。但是，由于其中一个透镜为负透镜，因此两个透镜之间的距离比开普勒式望远镜的透镜距离短。需要注意的是，使用两个透镜之间的有效焦距能够获得出色的近似总长度，而使用后焦距则能够获得准确的结果。

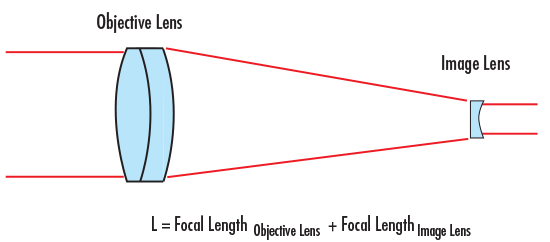
图2: 伽利略式望远镜

望远镜的放大倍数或放大倍数的倒数等于物镜焦距和目镜焦距的比值。

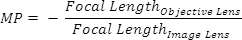
若放大倍数大于1，则望远镜将物体放大；若放大倍数小于1，则望远镜将物体缩小。

理论：

在结构中，物镜和成像透镜的位置颠倒。平行输入光束在开普勒式中集中在物镜和成像透镜之间的一个点上，进而形成一个激光能量聚焦的区域（图3）。该集中的点会加热透镜之间的空气，折射光路中的光线，而这有可能会造成波前误差。有鉴于此，大部分都选择使用伽利略式设计或其变体（图4）。

图3： 开普勒式

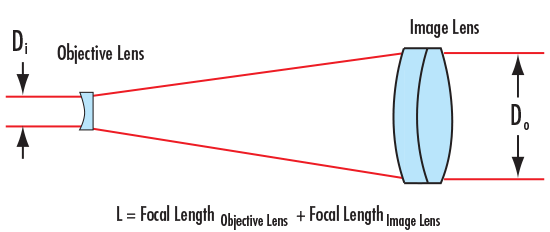
图4：伽利略式

使用开普勒式或伽利略式设计于应用时，重要的是能够计算出输出光束发散，这将决定了平行光线的偏差。光束发散取决于输出激光光束直径和输出激光光束直径。

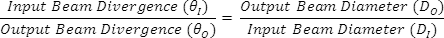
放大倍数(MP)现在即可依据光束发散或光束直径来表示。

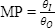
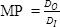
解上述方程式时，可以看到输出光束直径(DO)提高时，则输出光束发散减少，以此类推。所以，如果您将来缩小激光光束，光束直径将会缩小，但激光的光束发散将会提高。小光束的代价就是形成很大的扩张角。

除此之外，能够在特定工作距离(L)计算出输出光束直径也是极为重要的。输出光束直径是在特定工作距离(L)后输入光束直径和光束发散的函数（图5）。

Figure 5: Calculating the Output Beam Diameter at a Specific Working Distance

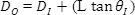
激光光束发散是以全角的，所以上述方程式是以θI表示，而非θI/2.。

由于会随放大倍数而提高输入光束，以及降低输入光束发散，因此将方程式(4)和(5)代入方程式(6)会获得如下结果。

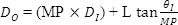
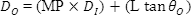
应用示例

示例1

以数值示例探究先前所述的方程式。

初始参数 放大倍数 = MP = 10X
输入光束直径 = 1mm
输入光束发散 = 1mrad
工作距离 = L = 100m

计算参数
输出光束直径

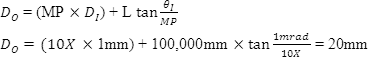
在不具备使用方程式(6)的的情况下，将此与光束直径相比较。

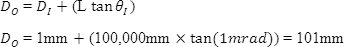
虽然会因特定的扩束功率而提高输入激光光束，但它也会因相同的扩束功率而降低光束发散，进而在较大距离下形成较小的平行光束。

示例2

使用在长工作距离中降低激光光束发散的理论示例。

为改善光束准直，可用于集中激光光束。下表显示了5X、10X和20X的的模拟聚焦性能。光斑尺寸的量度单位为微米，假设M2=1，使用直径为0.63mm，波长为632.8nm的激光光束，以此计算得出平行的输入光束。

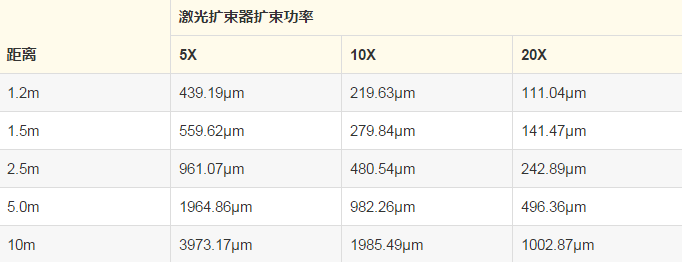
注意：上表所列的1/e2 光斑直径是从以下方程式计算得出：2 * f/# * 波长，f/#为工作f/#。